ソフトウエア Archive

皆さんこんにちは．
あっという間にゴールデンウイークも終わって，桜もちってしまいましたね

今回の話題は，ペーパークラフトです．
当社の要素技術の１つに，魚眼カメラ映像のような歪のある広角映像を扱うための画像処理技術があります．
歪を除去したり，パノラマ画像を生成したり，ステレオカメラを構成したりなど応用分野は多岐にわたります．

面白い活用方法はないものかと考えていたところ，１つひらめいたのがパノラマイメージのペーパークラフト．
ソフト開発のメンバーを焚きつけて全方位画像テクスチャーを正１２面体や正２０面体に展開するソフトを開発しちゃいました．

地元の観光名所などを魚眼カメラでパノラマ画像化して多面体のペーパークラフトを作ることができます．

今後，休日に自然豊かな岩手のあちこちの風景を撮影し正多面体展開図にして，ウエブサイトから皆様にお届けしていく予定でございます．

今回は，手始めに私たちの住む地球を正１２面体に展開してみました．
画像をクリックするとPDFをダウンロードできます．

作り方ですが．．．

①まずダウンロードしたPDFファイルを開いて，厚紙などへインクジェットプリンタを使って印刷します．
②はさみで地球の部分を切り出します．
③１つの面が５角形になっていますので辺をおっていきます．
④グレーのノリシロ部分をのりで貼って組み立ててれば完成

おおよそ３０分で組み立てることができます．
完成状態はこちら．

休日にお子様と一緒にペーパークラフト地球儀づくりはいかがでしょうか．

文責：鎌田 智也

自分が直面している問題の中に，最小二乗法のような最適化処理が含まれている場合，
それを解くための多くの真面目な(?)方法では
自分が最小化したい関数のGradient（関数を各パラメタで偏微分したもの）だとか
Hessian（それらをさらに偏微分したもの）だとかが必要になるので，
それらの大量の数式を計算するコードを用意せねばなりません．
そういった部分の実装は後でちゃんとやりたいという思いはあるのだけれども，
とりあえずまずは簡易的な実装で動きを見てみたい，ということが度々あります．

そんなときに使える方法として“Nelderの滑降シンプレックス法(Downhill Simplex Method)”があります．
この方法は，n次元のパラメタ空間の中に(n+1)個の頂点を持つSimplexとよばれる多面体みたいなものを用意して，これを頂点位置を変えながら変形させていくことでパラメタ値を更新していく，という探索法です．
他の方法と比べて遅いものの，
Gradient等を必要としないので比較的簡単に試してみることができるのが（＋アルゴリズムが直感的に分かりやすいのも）利点です．
で，この滑降シンプレックス法を使う機会が結構でてきたりしたので，基本動作部分をクラスにまとめてみました．

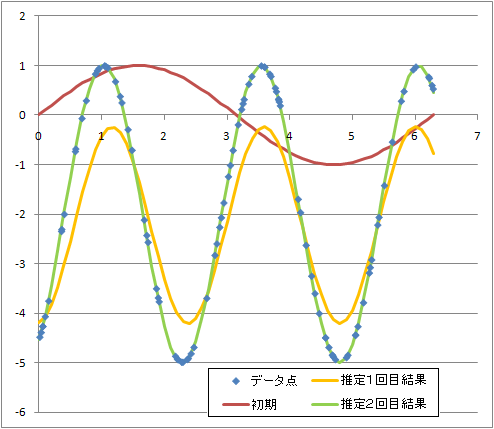
適当に動かしてみたサンプルの動作が↓のグラフです．
Nelder_Simplex（クラスとそれを使う適当なサンプルのソースコード）

データ点群（青）に対してsin波形な関数の当てはめを行っています．
赤がてきとーに与えた初期値での関数の様子です．（本当は，初期値はてきとーではダメ．）
どう見てもデータ点群に対するまともな初期値とは言い難い状態ですが，
走らせてみるとそこそこ頑張ってくれて，オレンジ色のグラフのようになりました．
この結果は初期値と比べると断然良いですが，もう少し頑張れそうなのに途中で力尽きた感があります．
そこで，滑降Simplex法での探索を，この結果を新たな初期値として再出発させてみると，
今度は緑色のグラフの結果に収束しました．

このように，滑降Simplex法（に限らずだと思いますが）では探索途中で動けなくなってしまう場合があるため，
止まった地点でSimplexを再構築して再出発させてみる必要があります．

パラメタ個数が少なくて計算時間があまり問題にならない場合や，他の解き方があるのだけれどもその実装を用意するのがめんどくさい，とかいう場面では結構使えると思います．

by nakiusagi3